Spontaneous magnetization is the appearance of an ordered spin state (magnetization) at zero applied magnetic field in a ferromagnetic or ferrimagnetic material below acritical point called the Curie temperature or TC.
Heated to temperatures above TC, ferromagnetic materials become paramagnetic and their magnetic behavior is dominated by spin waves or magnons, which are bosoncollective excitations with energies in the meV range. The magnetization that occurs below TC is a famous example of the “spontaneous” breaking of a global symmetry, a phenomenon that is described by Goldstone’s theorem. The term “symmetry breaking” refers to the choice of a magnetization direction by the spins, which have spherical symmetry above TC, but a preferred axis (the magnetization direction) below TC.
To first order, the temperature dependence of spontaneous magnetization at low temperatures is given by Bloch’s Law:
where M(0) is the spontaneous magnetization at absolute zero. The decrease in spontaneous magnetization at higher temperatures is caused by the increasing excitation of spin waves. In a particle description, the spin waves correspond to magnons, which are the massless Goldstone bosons corresponding to the broken symmetry. This is exactly true for an isotropic magnet.
Magnetic anisotropy, that is the existence of an easy direction along which the moments align spontaneously in the crystal, corresponds however to “massive” magnons. This is a way of saying that they cost a minimum amount of energy to excite, hence they are very unlikely to be excited as 
Near the Curie temperature,
where β is a critical exponent that depends on composition. The exponent is 0.34 for Fe and 0.51 for Ni.
An empirical interpolation of the two regimes is given by
it is easy to check two limits of this interpolation that follow laws similar to the Bloch law, for 

Ferromagnetism
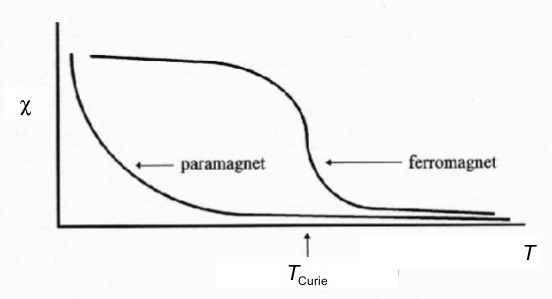
Ferromagnetism may be thought of as a special case of paramagnetism in which the individual spin magnetic moments interact (i.e. the moments are coupled). The uncompensated spins in individual atoms of a ferromagnetic material may couple either directly (direct exchange) or through an intermediate anion – usually oxygen (super exchange). In crystals of a ferromagnetic material, this gives rise to a net magnetic moment due to the coupling of spins in a preferred orientation (keep in mind that this coupling is quantum mechanical in nature and not purely due to the magnetic forces acting between neighboring atoms). As with paramagnets, ferromagnets have strong, positive magnetic susceptibility. Unlike paramagnets, when the applied field is removed, they retain a component of magnetization in the direction of the applied field – they are “permanently” magnetized (they do have hysteresis). Also, their susceptibility is not dependent upon temperature in a way that follows the Curie Law.
Temperature Dependence of Ferromagnetism
Since ferromagnetism results from the interaction of atomic moments in materials, there is an exchange energy associated with coupling the spin moments. At room temperature, this exchange energy is much greater than the energy due to randomizing thermal effects (kBT). If thermal energy exceeds the spin coupling (exchange) energy, the coupling breaks down and the material behaves as a paramagnet. This temperature is dependent on the material and is called the Curie temperature (or, in the case of antiferromagnetic materials, the Neél temperature).